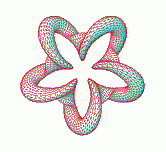Torsion is a difficult
property to observe directly. It has a sign, which distinguishes rolling
to the left from rolling to the right. We only visualize the unsigned
quantity, which we transform using f(x)=1+R*|x|.
The cross-section is an area preserving ellipse with aspect ratio
equal to f of the torsion at that point of the curve. The ellipse
does not rotate within its frame and the major axis is aligned with
the normal vector, N (s).
Note that if the number of times the curve winds around the meridian
is small but not too small, the torsion gets rather large when the
curve passes the narrow neck of the torus. This is reflected by a
skinny ellipse generating a pronounced ridge on the tube. We chose
to use two numbers to name each object, encoding the number of times
the curve winds around the length and around the meridian of the torus.

![]()