Moran process
I started this project during my internship almost three years ago. It's Pepa's project. His Ph.D. thesis was about that. I have results waiting to be published and some promising ideas about where to continue. But now, it's on hold.
Motivation
The model originated in biology. It describes how a mutant (a gene) with higher fitness spreads through a population. The population has a structure that influences the spread.
The mutants can be good bacteria (producing something we like), for instance. There we can think about how to help them by introducing structure.
Cells in our bodies also wage an evolutionary war. Cells with damaged DNA can turn into cancer. In other words, they became mutants and spread more. Some organs have a structure that blocks the spread of such mutants.
The models also describe how ideas or innovation spreads among people.
Model
Every vertex of a graph is occupied by one individual, either a resident or a mutant. Mutants have fitness r, and residents have fitness 1.
In one step of the process, we select an individual proportionally to the fitness. (Individual i is selected with probability equal to its fitness over the sum of all fitnesses in the graph) Then this individual spreads to a random neighbor.
We repeat these steps until one type becomes extinct and the other one wins (fixate).
We are interested in mutant's fixation probability (how likely mutants win). Another quantity is the time to the fixation that tells us how many steps we need for one type to fixate.
What is known
For the structureless case where everyone can replace everyone else, mutants fixate with probability 1-1/r. Some graphs help mutants more. We call them amplifiers. Others are called suppressors.
Sometimes the structure does a lot, sometimes not. For instance, any isothermal graph (every vertex gets killed with a similar probability) helps the mutant as the structureless case.
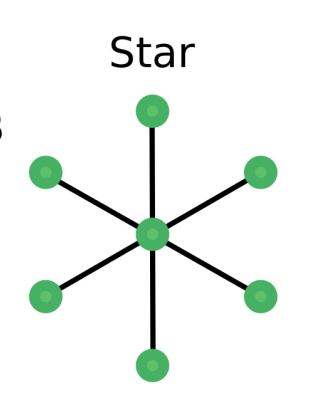
The first known amplifier was a star. One vertex connects to all others with no other connections. The mutant is very likely to appear in the leaf (not well-connected vertex) and then wait a long time to spread to another leaf through the center. The mutant with fitness r in this structure behaves as a mutant with fitness r^2 in the structureless case.
The ideas used in stars lead to graphs where one randomly placed mutant conquers everything with the probability of almost 1. These graphs exist (surprisingly) and are called superamplifiers.
death-Birth process
The process that we have dealt with so far is called Birth-death. First, we select an individual to spread, and then he kills a neighbor. It simulates a situation when resources are abundant (kill comes from the individual).
When resources are scarce, we can use the death-Birth process. First, one random individual dies, and then we select a neighbor according to the fitness to take up its space (kill comes from the environment).
For a complete graph, the two processes are indistinguishable. For the star, they are opposite (center is good in dB and bad in Bd).
One of the projects I'm working on is to create an amplifier graph for Birth-death and death-Birth at the same time. So far, we have failed, and I think there might not be one.
Coexistence
What we plan to publish soon is the question of coexistence. There, we have two environments, one beneficial to a mutant and one beneficial to the resident. Individuals can interact either inside one environment or across.
The question is, how long can sustain coexistence (both types living) based interactions parameters.
We characterized when the coexistence is exponential (long and desirable) and when it's just polynomial (short).
Glass dynamics
I started the project during my rotation with Maksym Serbyn. It's a work with him and people from his lab, so it's not going very fast. But I have some interesting observations and cute proofs that might be worth publishing.
Model
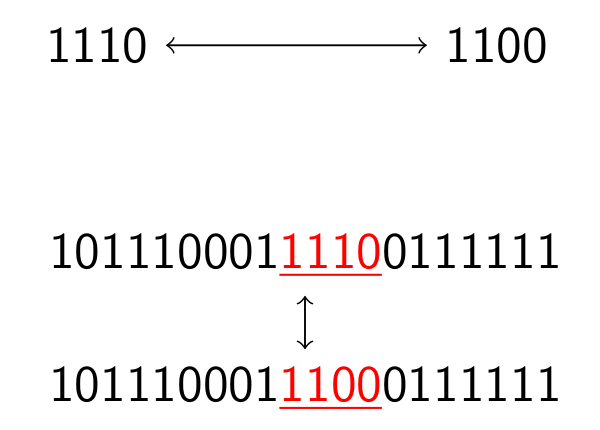
We have a long (denoted by n, but considered infinite) string S of 0's and 1's. Then we have several pairs P of binary strings with length k. Whenever there is a substring of S matching one element from P, we can substitute the substring with the other string from the same pair.
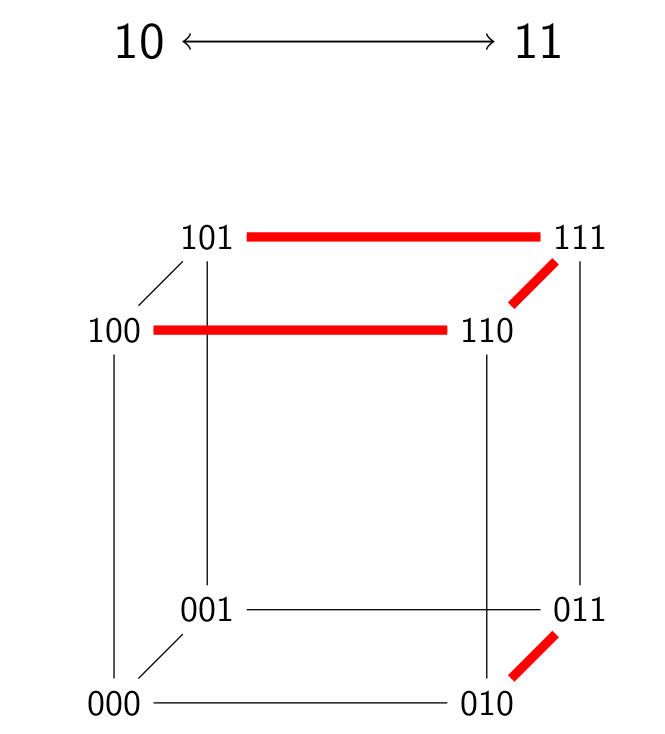
We imagine all possible (2^n) strings (length n) as vertices of a graph. Between two vertices, there is an edge if we can get from one string to the other by one pair substitution. We want to know how many components this graph has.
We cannot determine the exact number. Order of magnitude is enough for us. We distinguish three cases: just a few components, polynomially many in n, and exponentially many in n.
How to substitute and how to construct the graph is drawn on pictures on the left side.
Motivation
The model is called Glass dynamics. It models how glass is changing. When you see old glass, it is thicker at the bottom and generally uneven. It flows, and this model reflects that.
The numbers 0 or 1 corresponds to spins of atoms. There are rules when spins can change. Then glasses that have a different number of connected components behave differently.
I cannot motivate it well, but there is a motivation. I just don't know it. When I presented my preliminary results, Maksym sometimes stopped me and said something like: It corresponds to hessian in physics.
Results
I proved that the general problem is complex. If we have arbitrary pairs of sufficient length, the problem is PSPACE complete (more about complexity in the previous post here). It uses a standard reduction from a Turing machine and the fact that we can encode anything to a binary string. Since it's too hard, I'm interested in two simplifications.
In the first, the two elements of the pair are the same but differ only in the last bit (rightmost). That means we have a key, and if the string matches the key, we can change one bit.
In the second, all elements are the same except the last two, so we have a key followed by 01 or 10. That means, if the string matches the key, then we can flip the last two bits (this makes more sense in the motivation).
For the pairs that change only the last spin, I created an algorithm that computes the order of magnitude of components. I exploit the fact that we change only things on the right.
For the pairs that swap the last two spins, I have only some observations.
Then I thought about what we can say just from the number of pairs. If elements of pairs are long (thus hard to match), there must be many pairs; otherwise, the number of components is exponential.
Not only it is exponential, but the number of components of size 1 (strings that cannot be changed by any pair) is also exponential. The proof is nicely combinatoric. I'm looking forward to publishing it.